引言

不得不说，这绝对是是我并不长的CTF生涯中做过的最魔幻的一道逆向题。
看上去非常简单但就是做不来，由这道题也可以发现自己其实很多基础的知识也没有掌握好。
下来看了各位师傅的wp再加上自己操作了半天才搞明白是怎么回事。
pizzatql!!!

正片

dbl与输入的38位flag进行比较，嗯，显而易见。
mian
sub_13F3 函数，读入flag的两个字符转化成数字进行迭代运算，然后输出，嗯！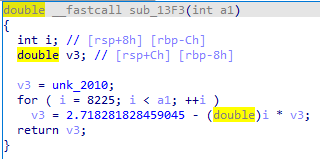
sub
unk数据不知道是多少，但是我们知道flag前两位肯定是‘fl’，于是我们决定写脚本反求unk的值，这里选用double浮点数并输出19位小数。

//注：以下为原理演示，非完整代码
//先介绍一下拼接函数，将a，b拼在一起，但因为是小端储存，所以最后输出要倒一下
//例：输入cpy(a,b) 输出9897
int cpy(int a,int b){
    int n,m;
    m = a / 10;
    if(m == 0) n = 10;
    else if(m > 0 && m < 10) n = 100;
    else n = 1000;
    return b * n + a;
}
//下面是逆推的一部分
for(int i = num - 1;i >=8225; i--)
        v = (2.718281828459045 - v) / i;
printf("%.19lf",v);

发现unk的值是0.0003304500204990972。
唉，这不就直接顺推爆破就行了嘛，于是写出爆破脚本输出：inf，inf，inf。。。
我直接？？？
行吧，可能是哪里内存炸了吧，想想看有没有其他路。
既然我们可以逆推算unk，有了unk我们也能逆推算flag吧，好的再写个脚本。

const double eps = 1e-8;
//a==b 浮点数降低误差比较
#define Equ(a,b) (fabs((a)-(b))<1e-8)

//布尔函数，num为cpy输出，如果该num经逆运算处理后符合unk，则为真，否则为假
bool cmp(int num,double a){
    double v = a;
    for(int i = num - 1;i >=8225; i--){
        v = (2.718281828459045 - v) / i;
    }
    if(Equ(v,unk)) return 1;
    else return 0;
}
//flag输出部分，a为dbl数组
for(int n = 0;n < 19; n+=2)
        for(int i = 32;i < 127; i++)
            for(int j = 32;j < 127; j++){
                int num = cpy(i,j);
                //printf("%d %d\n%d\n",i,j,num);
                if(cmp(num,a[n])){
                    flag[n] = i;
                    flag[n + 1] = j;
                }
            }
    printf("%s",flag);

结果，flag输出为“~~~~~~~~~~~~~~~”……
神奇的事情就来了，经过几次探索和研究大佬wp，最终发现，逆推函数，无论读入的字符串值为多少，
无论读入dbl数组的值为多少，最终v的值都会等于unk=0.0003304500204990972
wtf？？？为了更直观的表示，我们在逆推函数处理过程中打个表
附上完整打表脚本：

#include <stdio.h>
#include <math.h>
#include <windows.h>

const double eps = 1e-8;

//a==b
#define Equ(a,b) (fabs((a)-(b))<1e-8)
double unk = 0.0003304500204990972;
/*double func(int a1)
    {
        int i;
        double v3 = 0.0003304500204990972;
        
    for ( i = 8225; i < a1; ++i ){
        v3 = 2.718281828459045 - (double)i * v3;
        printf("%.19lf\n",v3);
    }
    return v3;
    }
*/

int cpy(int a,int b){
    int n,m;
    m = a / 10;
    if(m == 0) n = 10;
    else if(m > 0 && m < 10) n = 100;
    else n = 1000;
    return b * n + a;
}

bool cmp(int num,double a){
    double v = a;
    for(int i = num - 1;i >=8225; i--){
        v = (2.718281828459045 - v) / i;
        printf("%d %.19lf\n",i,v);
    }
    if(Equ(v,unk)) return 1;
    else return 0;
}

int main()
{
    double a[]={0.00009794904266317233, 0.00010270456917442, 0.00009194256152777895,0.0001090322021913372, 0.0001112636336217534, 0.0001007442677411854,0.0001112636336217534, 0.0001047063607908828, 0.0001112818534005219,0.0001046861985862495, 0.0001112818534005219, 0.000108992856167966,0.0001112636336217534, 0.0001090234561758122, 0.0001113183108652088,0.0001006882924839248, 0.0001112590796092291, 0.0001089841164633298,0.00008468431512187874};
    char flag[38]={},dflag[38]={};
    /*for(int n = 0;n < 19; n+=2)
        for(int i = 32;i < 127; i++)
            for(int j = 32;j < 127; j++){
                int num = cpy(i,j);
                //printf("%d %d\n%d\n",i,j,num);
                if(cmp(num,a[n])){
                    flag[n] = i;
                    flag[n + 1] = j;
                }
            }
    printf("%s",flag);*/
    int s1 = 'z',s2 = 'z';
    int num = cpy(s1,s2);
    int k = cmp(num,a[1]);
    printf("%d\n",k);

    
    system("pause");
        
return 0;
}
//若是dbl[1]则121121位后五位0.0000222580811153681 0.0000222589221288727 0.0000222591043943769 0.0000222592866682606 0.0000222594689451295
//若是dbl[0]则121121位后五位0.0000222581200564717 0.0000222589221285538 0.0000222591043943769 0.0000222592866682606 0.0000222594689451295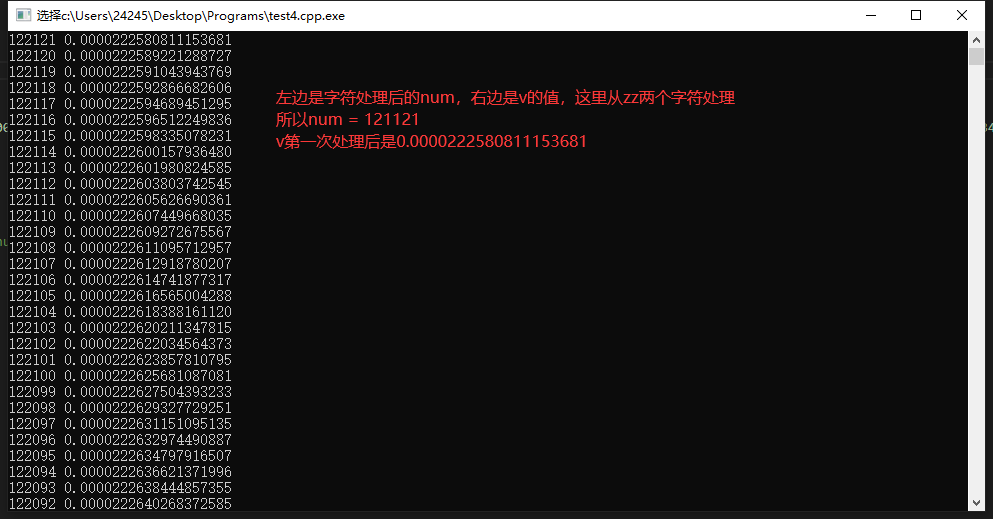

test1
替换dbl值比较发现从最开始处理三位后，就因为精度的问题后面每一个值都与i值一一对应，直到8225位时正好时unk的值
test2
那么我们可以发现，这就像数组一样，与i一一对应。
例如：
当输入fl时，正好对应i值108102，而此时对应的值正好是dbl[0] = 0.00009794904266317233.
也就是v[108102] = 0.00009794904266317233；
那么我们将dbl后面的数在这个数组里一一对应的i值找出来，对应成字符并拼接，就可以得出flag
思路大概就是这样，（我觉得已经讲的非常清楚了）
最后的解密脚本不想写了，直接附上答案：flag{saam_dim_gei_lei_jam_caa_sin_laa}

一些小总结（吐槽）

所以这到底是个什么鬼题？考智商的吧……
其实最开始是卡在一个非常蠢的点上的：sub_13F3居然是读入两个字符……
证据就是ida括号里写着的数据大小。从此以后ida自己给的数据类型我是一个字都不会信了
还有，unk就是unknown，本来要靠动调之类的调出来的，比如这题内存中的unk值根本就不是求出来的那个
这份wp只是我自己总结的一点思路，参考参考就好，其他师傅们还有更多神奇的解法，我太菜了自然是看不懂了，嗯！
就这样吧，摸了。